Тип
|
Задание
|
B1
|
| Билет на автобус стоит 110 рублей. Ожидается повышение цены на 10%. Какое наибольшее число билетов можно будет купить на 1000 рублей? |
|
B2
|
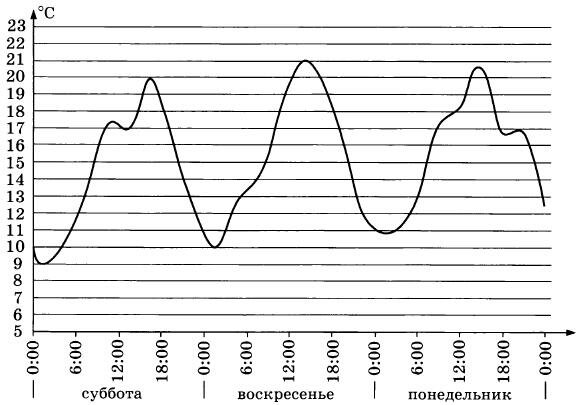
На графике показано изменение температуры воздуха в некотором населенном пункте на протяжении трех суток, начиная с 0 часов субботы. На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха в ночь с субботы на воскресенье. Ответ дайте в градусах Цельсия.
 |
|
B3
|
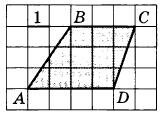
Найдите площадь трапеции ABCD.
 |
|
B4
|
| Семья из трех человек едет из Москвы в Бологое. Можно ехать поездом, а можно на своей машине. Билет на поезд стоит 325 рублей на одного человека. Автомобиль расходует 11 литров бензина на 100 километров пути, расстояние по шоссе равно 350 км, а цена бензина равна 19 рублей за литр. Какова наименьшая стоимость (в рублях) семейной поездки? |
|
B5
|
Решите уравнение
\( log_{2} x = 5 \) |
|
B6
|
| Окружность, вписанная в треугольник ABC, касается сторон АВ, ВС и АС в точках М, К и Р соответственно. Найдите периметр треугольника ABC, если АР = 5, ВМ = 6, СК = 7. |
|
B7
|
Вычислите
\( log_{6} 144 - log_{6} 4 \) |
|
B8
|
На рисунке изображены график функции у = f(x) — производной функции f(x), и восемь точек на оси абсцисс: x1, х2, х3, ..., х8-Сколько из этих точек принадлежат промежуткам убывания функции?
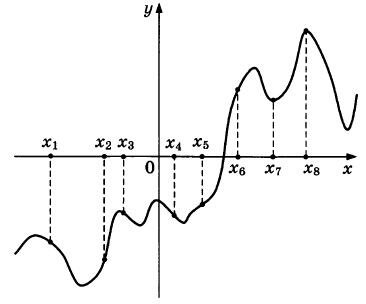 |
|
B9
|
| Расстояние между скрещивающимися ребрами правильной треугольной пирамиды равно 12, а синус угла между боковым ребром и плоскостью основания равен 0,3. Найдите высоту основания пирамиды. |
|
B10
|
| На соревнования по метанию диска приехали 6 спортсменов из Швейцарии, 3 из Болгарии и 6 из Австрии. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что третьим будет выступать спортсмен из Болгарии. |
|
B11
|
| Площадь боковой поверхности конуса равна 10 см2. Радиус основания конуса увеличили в 6 раз, а образующую уменьшили в 4 раза. Найдите площадь боковой поверхности получившегося конуса. Ответ дайте в см2. |
|
B12
|
| Температуру нагревательного элемента (в градусах Кельвина) в зависимости от времени (в минутах) можно вычислять по формуле T(t) = Т0 + at + bt2, где Т0 = 760 К, а = 34 К/мин, b = -0,2 К/мин2. Известно, что при температурах нагревателя свыше 1600 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время (в минутах) после начала работы нужно отключать прибор. |
|
B13
|
| Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 90 км/ч, а вторую половину времени — со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. |
|
B14
|
Найдите наименьшее значение функции у = 13-7 sin х - 9х на отрезке
\( \left[ - \frac{3 \pi}{2} ; 0 \right] \) |
|
C1
|
Решите уравнение
\( \frac{(tg x + \sqrt{3} ) log_{13} ( 2sin^{2} x)}{log_{31} (\sqrt{2} cos x)} = 0 \) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C2
|
| В правильной шестиугольной призме A...F1 все ребра которой равны 1, найдите тангенс угла между плоскостями ABC и DB1F1. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C3
|
Решите систему неравенств
\( \left\{ \begin{eqnarray} x^{2} + 6^{x} + 4 \leq 44 \cdot \log_{5} (x+3), \\ 4x + 6^{x} \geq 44 \cdot \log_{5} (x+3). \\ \end{eqnarray} \right. \) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C4
|
| На сторонах АВ, ВС и АС треугольника ABC взяты соответственно точки К, L и М, причем АК : КВ = 2:3, BL : LC = 1:2, СМ : МА = 3 : 1. В каком отношении отрезок KL делит отрезок ВМ? |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C5
|
Найдите все значения параметра а, при каждом из которых имеет единственное решение (х; у) система уравнений
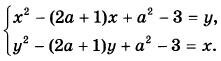 |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C6
|
Найдите наименьшее и наибольшее натуральные значения n, при которых уравнение
\((х^{2} + у^{2})^{2010} = х^{n} • у^{n} \)
имеет натуральные решения. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|