Тип
|
Задание
|
B1
|
| Билет на автобус стоит 15 рублей. Какое максимальное число билетов можно будет купить на 100 рублей после повышения цены билета на 20%? |
|
B2
|
На диаграмме показана среднемесячная температура воздуха (в градусах Цельсия) в Ярославле по результатам многолетних наблюдений. Найдите по диаграмме количество месяцев, когда средняя температура в Ярославле была отрицательной.
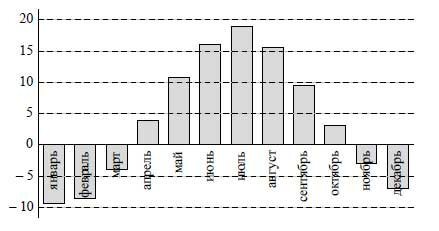 |
|
B3
|
Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки 1 см ? 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах.
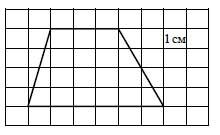 |
|
B4
|
Строительная фирма планирует купить 70 м3 пеноблоков у одного из трёх поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой?
| Поставщик |
Стоимость пеноблоков (руб. за 1 м3) |
Стоимость доставки (руб.) |
Дополнительные условия доставки |
| A |
2 600 |
10 000 |
Нет |
| Б |
2 800 |
8 000 |
При заказе товара на сумму свыше 150 000 рублей доставка бесплатная |
| В |
2 700 |
8 000 |
При заказе товара на сумму свыше 200 000 рублей доставка бесплатная |
|
|
B5
|
| Найдите корень уравнения \(\log_{3}(x-3)=2\) |
|
B6
|
| Треугольник ABC вписан в окружность с центром O. Найдите угол BOC , если угол BAC равен 32°. |
|
B7
|
| Найдите \(\sin(\alpha)\) , если \(\cos(\alpha)=0,6\) и \(\pi < \alpha < 2\pi\) |
|
B8
|
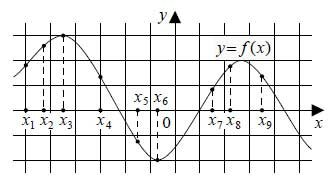
На рисунке изображён график дифференцируемой функции \(y = f(x)\). На оси абсцисс отмечены девять точек: \(x1, x2, x3, ..., x9\). Среди этих точек найдите все точки, в которых производная функции \(f(x)\) отрицательна. В ответе укажите количество найденных точек.
 |
|
B9
|
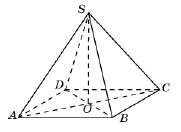
Диагональ AC основания правильной четырёхугольной пирамиды SABCD равна 6. Высота пирамиды SO равна 4. Найдите длину бокового ребра SB.
 |
|
B10
|
| В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете не будет вопроса о грибах. |
|
B11
|
| Объём первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м3). |
|
B12
|
| Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой \(h(t) = ?5t^2 +18t\), где h – высота в метрах, t – время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров. |
|
B13
|
| Весной катер идёт против течения реки в \(1\frac{2}{3}\) раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в \(1\frac{1}{2}\) раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч). |
|
B14
|
Найдите наибольшее значение функции
\(y = 2\cos(x) + \sqrt{3}x - \frac{\sqrt{3}\pi}{3}\) на отрезке \(\left[0;\frac{\pi}{2}\right]\) |
|
C1
|
а) Решите уравнение
\(\cos 2x = 1 - \cos\left(\frac{\pi}{2}-x\right)\)
б) Найдите все корни этого уравнения, принадлежащие промежутку \(\left[-\frac{5\pi}{2};-\pi\right]\) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C2
|
| Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а диагональ боковой грани равна \(\sqrt{5}\). Найдите угол между плоскостью A1BC и плоскостью основания призмы. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C3
|
Решите систему неравенств
\(\left\{ \begin{eqnarray} 4^{x} \leq 9 \cdot 2^{x} + 22, \\ \log_{3}(x^2 - x - 2) \leq 1 + \log_{3}\frac{x+1}{x-2}. \\ \end{eqnarray} \right.\) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C4
|
| На стороне BA угла ABC , равного 30°, взята такая точка D, что AD = 2 и BD =1. Найдите радиус окружности, проходящей через точки A, D и касающейся прямой BC. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C5
|
Найдите все значения a, при каждом из которых наименьшее значение функции
\(f(x) = 2ax + |x^2 - 8x + 7|\)
больше 1. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C6
|
На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно -3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно -8.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них? |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|