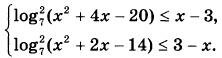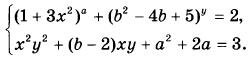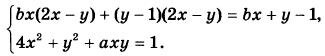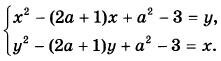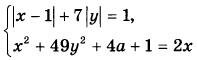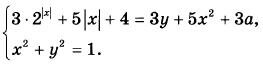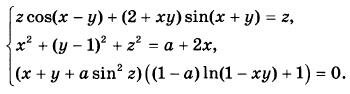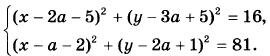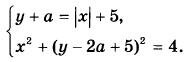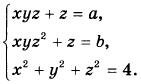Тип
|
Задание
|
|
|
| Дроби, проценты, рациональные числа. |
| Школа закупает книги по цене 50 рублей за штуку. При покупке больше 10 штук магазин дает скидку 10%. Сколько книг можно купить на 1000 рублей? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Дроби, проценты, рациональные числа. |
| Пакет молока стоит 21 рубль 30 копеек. Сколько пакетов молока можно купить на 500 рублей? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Дроби, проценты, рациональные числа. |
| Билет на автобус стоит 110 рублей. Ожидается повышение цены на 10%. Какое наибольшее число билетов можно будет купить на 1000 рублей? |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
| Больному прописан курс лекарства, которое нужно принимать по 250 мг два раза в день в течение 7 дней. В одной упаковке лекарства содержится 10 таблеток по 125 мг. Какое наименьшее количество упаковок понадобится на весь курс лечения? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Дроби, проценты, рациональные числа. |
| Школа закупает книги по цене 70 рублей за штуку. При покупке на сумму больше 500 рублей магазин дает скидку 10%. Сколько рублей будет стоить покупка 23 книг? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Дроби, проценты, рациональные числа. |
| В туристический поход на 7 дней отправляется группа из 8 человек. В походе на одного человека приходится 90 грамм сахара в день. Сколько трехкилограммовых мешков сахара нужно купить, чтобы сахара хватило на весь поход? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Дроби, проценты, рациональные числа. |
| Пачка масла стоит 37 рублей 70 копеек. Сколько пачек масла можно купить на 500 рублей? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Дроби, проценты, рациональные числа. |
| В двух автомобилях перевозилось одинаковое количество помидоров. При этом в первом автомобиле при транспортировке испортилось 20% перевозимых помидоров, что составило 96 штук. Во втором автомобиле испортилось 15% помидоров. Сколько помидоров испортилось во втором автомобиле? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Дроби, проценты, рациональные числа. |
| В туристический поход отправляется группа из 18 человек. В походе на одного человека приходится 60 грамм гречки на прием пищи. Планируется 7 раз готовить гречку. Сколько килограммовых пачек необходимо купить, чтобы гречки хватило? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Дроби, проценты, рациональные числа. |
| В летнем лагере на каждого участника полагается 30 г сахара в день. В лагере 223 человека. Сколько килограммовых упаковок сахара понадобится на весь лагерь на 8 дней? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графическое представление данных. Анализ данных. |
На диаграмме показана среднемесячная температура воздуха в Париже за каждый месяц 2009 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев в 2009 году, когда среднемесячная температура была равна 10 градусам Цельсия.
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графическое представление данных. Анализ данных. |
Первый посев семян петрушки рекомендуется проводить в апреле при дневной температуре воздуха не менее +6 °С. На рисунке показан прогноз дневной температуры воздуха на первые три недели апреля. Определите, в течение скольких дней за этот период можно производить посев петрушки.
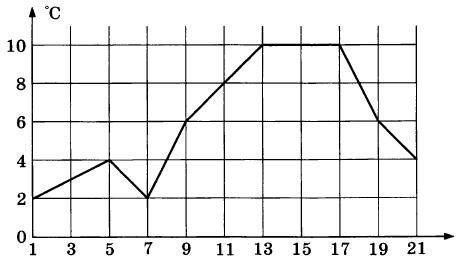 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графическое представление данных. Анализ данных. |
На графике показано изменение температуры воздуха в некотором населенном пункте на протяжении трех суток, начиная с 0 часов субботы. На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха в ночь с субботы на воскресенье. Ответ дайте в градусах Цельсия.
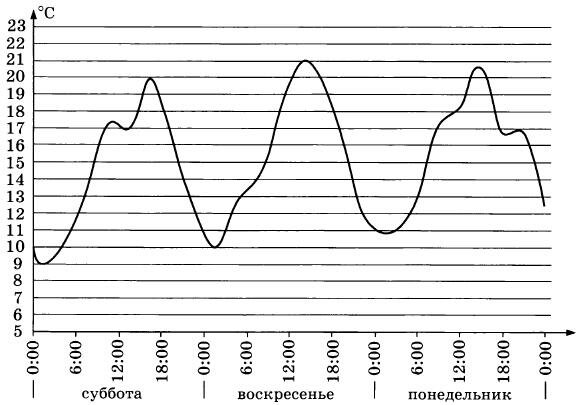 |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
На диаграмме показано число запросов со словом ЕГЭ, сделанных на некотором поисковом сайте во все месяцы с января по декабрь 2009 года. По горизонтали указываются месяцы, по вертикали — число запросов за данный месяц. Определите по диаграмме, во сколько раз максимальное месячное число запросов превышало минимальное месячное число запросов со словом ЕГЭ в 2009 году.
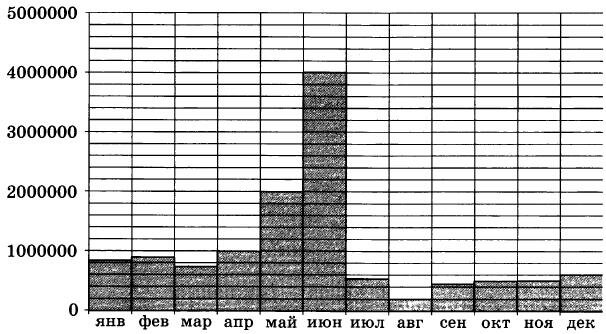 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графическое представление данных. Анализ данных. |
На диаграмме показано число запросов со словом КИНО, сделанных на некотором поисковом сайте во все месяцы с января по сентябрь 2010 года. По горизонтали указываются месяцы, по вертикали — число запросов за данный месяц. Определите по диаграмме наибольшее месячное число запросов со словом КИНО в указанный период.
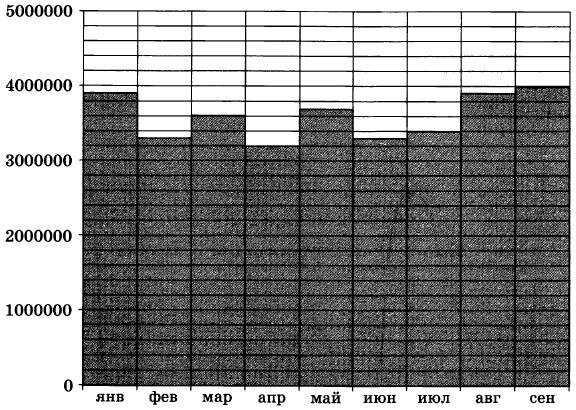 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графическое представление данных. Анализ данных. |
На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций газодобывающей компании в первые две недели апреля. В первую неделю апреля бизнесмен купил 14 акций, а потом продал их на второй неделе. Какую наибольшую прибыль он мог получить? Ответ дайте в рублях.
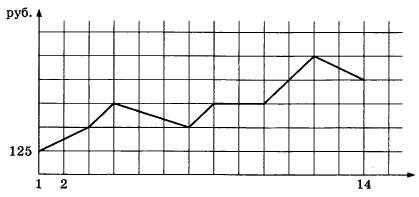 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графическое представление данных. Анализ данных. |
На диаграмме показана среднемесячная температура воздуха в Хельсинки за каждый месяц 2009 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев в 2009 году, когда среднемесячная температура была отрицательная.
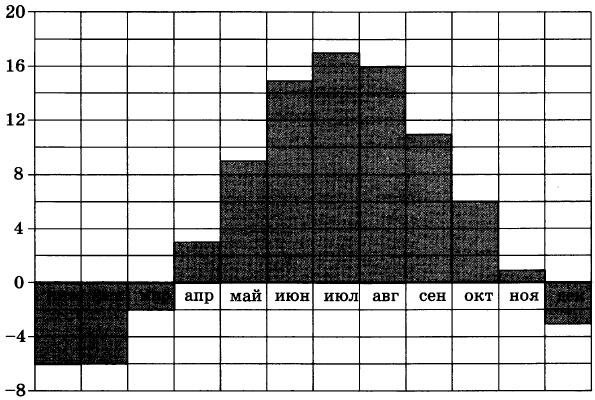 |
| Подробнее | Комментировать | Сохранить |
|
|
|
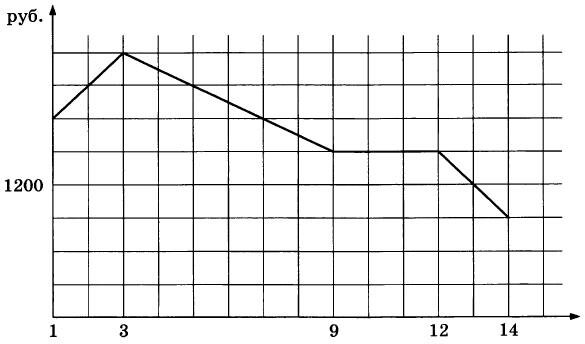
| Графическое представление данных. Анализ данных. |
На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций газодобывающей компании в первые две недели ноября. 2 ноября бизнесмен приобрел 10 акций этой компании. Шесть из них он продал 6 ноября, а 13 ноября — остальные 4. Сколько рублей потерял бизнесмен в результате этих операций?
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
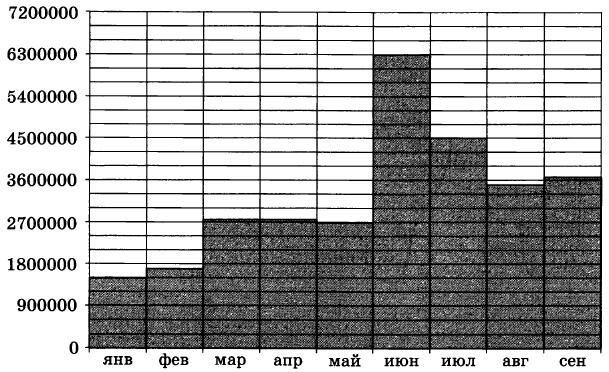
| Графическое представление данных. Анализ данных. |
На диаграмме показано число запросов со словом ФУТБОЛ, сделанных на некотором поисковом сайте во все месяцы с января по сентябрь 2010 года. По горизонтали указываются месяцы, по вертикали — число запросов за данный месяц. Определите по диаграмме, сколько было месяцев в указанный период, когда число запросов со словом ФУТБОЛ было меньше 3600000.
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
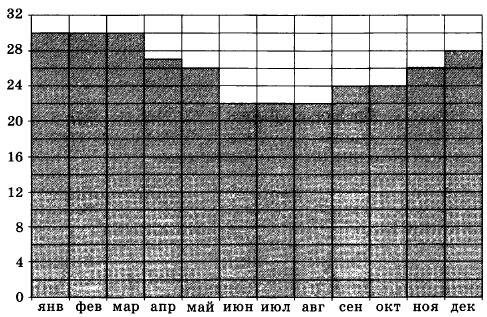
| Графическое представление данных. Анализ данных. |
На диаграмме показана среднемесячная температура воздуха в Рио-де-Жанейро за каждый месяц 2009 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячной температурой в 2009 году. Ответ дайте в градусах Цельсия.
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
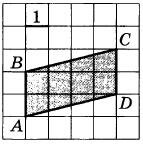
| Площадь треугольника, параллелограмма, трапеции, круга, сектора. Декартовы координаты на плоскости. |
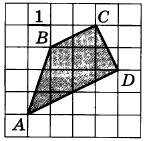
Найдите площадь параллелограмма ABCD.
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Площадь треугольника, параллелограмма, трапеции, круга, сектора. Декартовы координаты на плоскости. |
Найдите площадь трапеции ABCD.
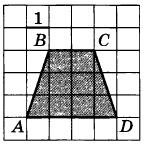 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Площадь треугольника, параллелограмма, трапеции, круга, сектора. Декартовы координаты на плоскости. |
Найдите площадь трапеции ABCD.
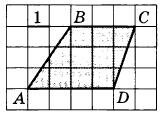 |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
|
|
| Площадь треугольника, параллелограмма, трапеции, круга, сектора. Декартовы координаты на плоскости. |
Найдите площадь S круга. В ответе укажите \(\frac{S}{\pi}\)
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Площадь треугольника, параллелограмма, трапеции, круга, сектора. Декартовы координаты на плоскости. |
Найдите площадь трапеции ABCD.
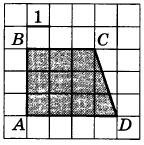 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Площадь треугольника, параллелограмма, трапеции, круга, сектора. Декартовы координаты на плоскости. |
Найдите площадь квадрата ABCD.
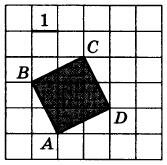 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Площадь треугольника, параллелограмма, трапеции, круга, сектора. Декартовы координаты на плоскости. |
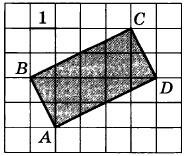
Найдите площадь прямоугольника ABCD.
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Площадь треугольника, параллелограмма, трапеции, круга, сектора. Декартовы координаты на плоскости. |
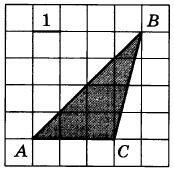
Найдите площадь треугольника ABC
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Площадь треугольника, параллелограмма, трапеции, круга, сектора. Декартовы координаты на плоскости. |
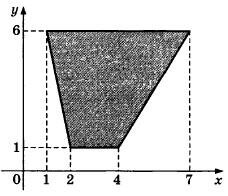
Найдите площадь трапеции, вершинами которой являются точки с координатами (1; 6), (7; 6), (4; 1), (2; 1).
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Табличное представление данных. Прикладные задачи на нахождение наибольшего и наименьшего значения |
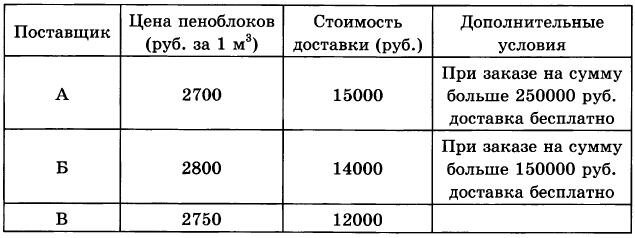
Строительная фирма собирается приобрести 85 кубометров пеноб-локов у одного из трех поставщиков. Цены на пеноблоки и условия доставки приведены в таблице. Какова наименьшая стоимость такой покупки с доставкой (в рублях)?
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Табличное представление данных. Прикладные задачи на нахождение наибольшего и наименьшего значения |
Для транспортировки 50 тонн груза на 900 км можно использовать одного из трех перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого из них указаны в таблице. Сколько будет стоить самый дешевый вариант перевозки (в рублях)?
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Табличное представление данных. Прикладные задачи на нахождение наибольшего и наименьшего значения |
| Семья из трех человек едет из Москвы в Бологое. Можно ехать поездом, а можно на своей машине. Билет на поезд стоит 325 рублей на одного человека. Автомобиль расходует 11 литров бензина на 100 километров пути, расстояние по шоссе равно 350 км, а цена бензина равна 19 рублей за литр. Какова наименьшая стоимость (в рублях) семейной поездки? |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
На рисунке показаны схема дорог и расстояние в километрах между населенными пунктами А, В, С, D и Е вдоль этих дорог. Мопед, грузовик и автобус одновременно выезжают из города А и добираются в город Е разными путями. Мопед едет через поселки С и В, грузовик — только через В, а автобус едет через город D. Мопед был в пути 1 час 20 минут, грузовик — 1 час, а автобус — 1 час 40 минут. Найдите среднюю скорость того транспортного средства, у которого эта скорость наибольшая. Ответ дайте в км/ч.
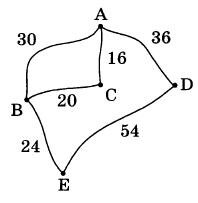 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Табличное представление данных. Прикладные задачи на нахождение наибольшего и наименьшего значения |
При заказе дисков в некотором шведском музыкальном магазине цена одного диска не зависит от количества дисков в заказе, а доставка заказа в другие страны осуществляется на таких условиях:
доставка заказа не более чем из трех дисков — 6 $;
доставка заказа от 4 до 8 дисков — 17,5 $;
доставка заказа из 9 и более дисков — 28 $.
Сколько долларов придется заплатить за доставку самым дешевым способом (можно в несколько заказов) при приобретении ровно 9 дисков? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Табличное представление данных. Прикладные задачи на нахождение наибольшего и наименьшего значения |
Строительной фирме нужно приобрести 60 кубометров пеноблоков у одного из трех поставщиков. Какова наименьшая стоимость (в рублях) покупки с доставкой, если цены на пеноблоки и условия доставки приведены в таблице?
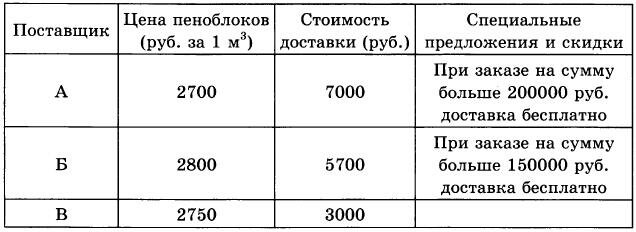 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Табличное представление данных. Прикладные задачи на нахождение наибольшего и наименьшего значения |
Для транспортировки 80 тонн груза на 1100 км можно использовать одного из трех перевозчиков. Тарифы перевозчиков приведены в таблице. Какова наименьшая стоимость (в рублях) транспортировки?
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Табличное представление данных. Прикладные задачи на нахождение наибольшего и наименьшего значения |
При заказе дисков в некотором шведском музыкальном магазине цена одного диска не зависит от количества дисков в заказе, а доставка заказа в другие страны осуществляется на таких условиях:
доставка заказа не более чем из трех дисков — 6 $;
доставка заказа от 4 до 8 дисков — 17,5 $;
доставка заказа из 9 и более дисков — 28 $.
Сколько долларов придется заплатить за доставку самым дешевым способом (можно в несколько заказов) при приобретении ровно 11 дисков? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Табличное представление данных. Прикладные задачи на нахождение наибольшего и наименьшего значения |
| Ткань можно покупать либо по метру, стоимостью 23 рубля за метр, либо рулонами по 100 метров, стоимостью 1950 рублей за рулон. Сколько рублей придется заплатить за самый дешевый вариант приобретения 80 метров ткани? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Табличное представление данных. Прикладные задачи на нахождение наибольшего и наименьшего значения |
В таблице указаны средние цены (в рублях) на некоторые основные продукты питания в трех городах России (по данным на начало 2010 года).
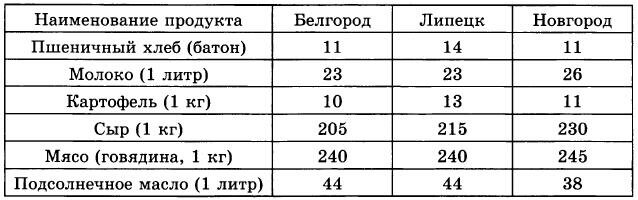
Определите, в каком из этих городов окажется самым дешевым следующий набор продуктов: 2 батона пшеничного хлеба, 3 кг говядины, 1 л подсолнечного масла. В ответ запишите стоимость данного набора продуктов в этом городе (в рублях). |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Планиметрия. Треугольник, трапеция, параллелограмм, ромб, прямоугольник, квадрат. Окружность и круг. Угол. Нахождение элементов и величин в |
| Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК = 7, СК = 8. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Планиметрия. Треугольник, трапеция, параллелограмм, ромб, прямоугольник, квадрат. Окружность и круг. Угол. Нахождение элементов и величин в |
| В треугольнике ABC углы А и В равны соответственно 45° и 67°. Найдите угол между биссектрисой и высотой, проведенными из вершины С. Ответ дайте в градусах. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Планиметрия. Треугольник, трапеция, параллелограмм, ромб, прямоугольник, квадрат. Окружность и круг. Угол. Нахождение элементов и величин в |
| Окружность, вписанная в треугольник ABC, касается сторон АВ, ВС и АС в точках М, К и Р соответственно. Найдите периметр треугольника ABC, если АР = 5, ВМ = 6, СК = 7. |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
|
|
| Планиметрия. Треугольник, трапеция, параллелограмм, ромб, прямоугольник, квадрат. Окружность и круг. Угол. Нахождение элементов и величин в |
| В прямоугольном треугольнике высота, проведенная к гипотенузе, делит прямой угол на два угла, один из которых равен 56°. Найдите меньший угол данного треугольника. Ответ дайте в градусах. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Планиметрия. Треугольник, трапеция, параллелограмм, ромб, прямоугольник, квадрат. Окружность и круг. Угол. Нахождение элементов и величин в |
| Концы отрезка АВ лежат по разные стороны от прямой l. Расстояние от точки А до прямой l равно 7, а расстояние от точки В до прямой l равно 13. Найдите расстояние от середины отрезка АВ до прямой l. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Планиметрия. Треугольник, трапеция, параллелограмм, ромб, прямоугольник, квадрат. Окружность и круг. Угол. Нахождение элементов и величин в |
| Отрезок АВ является хордой окружности с центром О. Найдите угол между прямой АВ и касательной к окружности, проходящей через точку А, если угол АОВ равен 56°. Ответ дайте в градусах. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Планиметрия. Треугольник, трапеция, параллелограмм, ромб, прямоугольник, квадрат. Окружность и круг. Угол. Нахождение элементов и величин в |
| Диагонали трапеции AJBCD с основаниями АВ и CD пересекаются в точке М. Найдите МС, если АВ = 11, DC = 33, АС = 28. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Планиметрия. Треугольник, трапеция, параллелограмм, ромб, прямоугольник, квадрат. Окружность и круг. Угол. Нахождение элементов и величин в |
| Найдите число сторон правильного многоугольника, каждый из углов которого равен 140°. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Планиметрия. Треугольник, трапеция, параллелограмм, ромб, прямоугольник, квадрат. Окружность и круг. Угол. Нахождение элементов и величин в |
| Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 11, а одна из диагоналей ромба равна 44. Найдите величину тупого угла ромба. Ответ дайте в градусах. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа, корни и степени. Основы тригонометрии. Логарифмы. Преобразования выражений. |
Вычислите
\(log_{5} 135 - log_{5} 5,4\) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа, корни и степени. Основы тригонометрии. Логарифмы. Преобразования выражений. |
Найдите значение выражения
\( log_{4} 104 - log_{4} 6,5 \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа, корни и степени. Основы тригонометрии. Логарифмы. Преобразования выражений. |
Вычислите
\( log_{6} 144 - log_{6} 4 \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа, корни и степени. Основы тригонометрии. Логарифмы. Преобразования выражений. |
Найдите значение выражения
\(\frac{28}{2^{log_{2} 7}}\) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа, корни и степени. Основы тригонометрии. Логарифмы. Преобразования выражений. |
Найдите значение выражения
\(log_{6} 126 - log_{6} 3,5 \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа, корни и степени. Основы тригонометрии. Логарифмы. Преобразования выражений. |
| Найдите значение выражения \(\frac{60}{6^{log_{6} 5}}\) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа, корни и степени. Основы тригонометрии. Логарифмы. Преобразования выражений. |
Найдите значение выражения
\(\frac{30}{5^{log_{5} 3}} \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа, корни и степени. Основы тригонометрии. Логарифмы. Преобразования выражений. |
Найдите значение выражения
\(log_{6} 144 - log_{6} 4 \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа, корни и степени. Основы тригонометрии. Логарифмы. Преобразования выражений. |
| Найдите значение выражения \(log_{3} 13 - log_{3} 117\) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа, корни и степени. Основы тригонометрии. Логарифмы. Преобразования выражений. |
Найдите значение выражения
\((558^2 - 23^2) : 581 \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графики функции, производных функций. Исследование функций. |
На рисунке изображен график функции у = f(x). Прямая, проходящая через точку (-2; 4), касается этого графика в точке с абсциссой 2. Найдите f'(2).
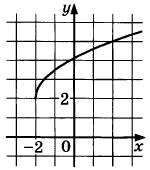 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графики функции, производных функций. Исследование функций. |
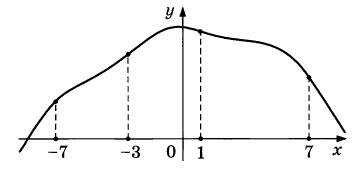
На рисунке изображен график функции у = f(x) и отмечены точки -7, -3, 1, 7. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графики функции, производных функций. Исследование функций. |
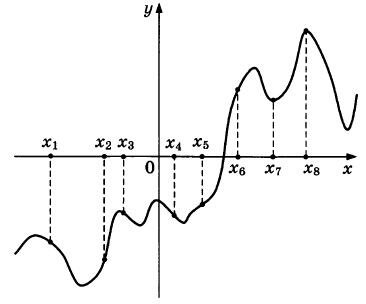
На рисунке изображены график функции у = f(x) — производной функции f(x), и восемь точек на оси абсцисс: x1, х2, х3, ..., х8-Сколько из этих точек принадлежат промежуткам убывания функции?
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графики функции, производных функций. Исследование функций. |
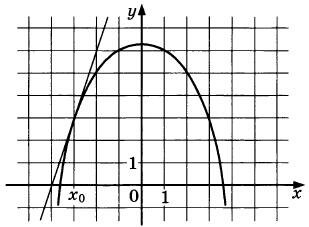
На рисунке изображены график функции у = f(x) и касательная к нему в точке с абсциссой f'(x) Найдите значение производной f(x) в точке x0.
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графики функции, производных функций. Исследование функций. |
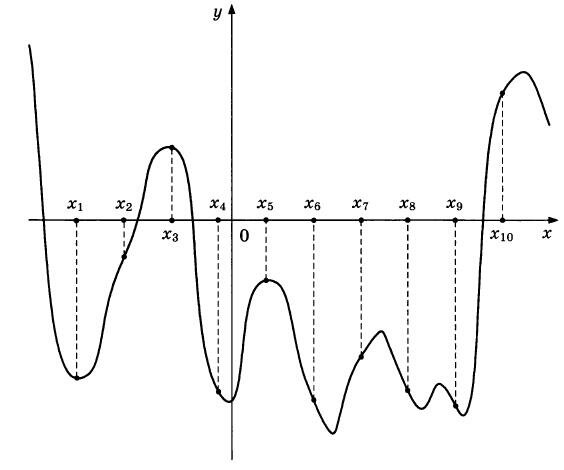
На рисунке изображены график функции у = f(x) и десять точек на оси абсцисс: х1, х2, x3..,x10 В скольких из этих точек производная функции f(x) отрицательна?
 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графики функции, производных функций. Исследование функций. |
На рисунке изображен график функции у = f(x) и отмечены точки -5, -3, 3, 7. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
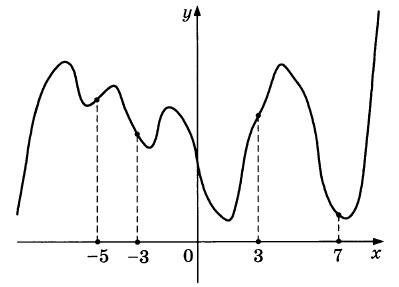 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графики функции, производных функций. Исследование функций. |
На рисунке изображен график функции у — f(x). Прямая, проходящая через точку (-1; 1), касается этого графика в точке с абсциссой 3. Найдите f'(3).
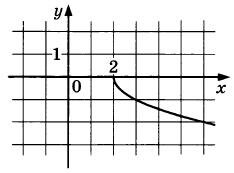 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графики функции, производных функций. Исследование функций. |
На рисунке изображен график функции у = f(x). Прямая, проходящая через точку (-6; -1), касается этого графика в точке с абсциссой 6. Найдите f(6).
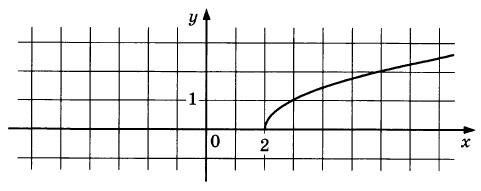 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графики функции, производных функций. Исследование функций. |
На рисунке изображены график функции у = f’(x) — производной функции f(x), и семь точек на оси абсцисс: х1 х1, х2, ..., х7. В скольких из этих точек функция f(x) возрастает?
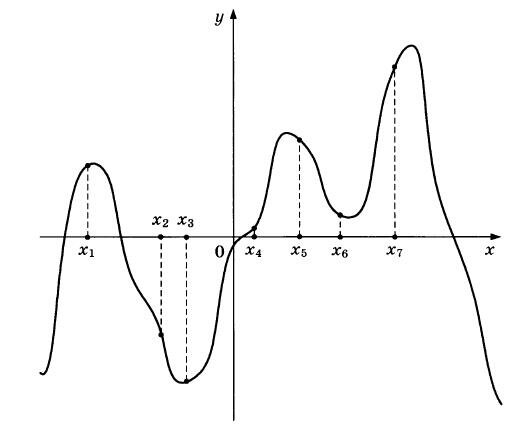 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Графики функции, производных функций. Исследование функций. |
На рисунке изображены график функции у= f(x) и десять точек на оси абсцисс: x1, x2, х3, ..., x10. В скольких из этих точек производная f(x) функции f(x) положительна?
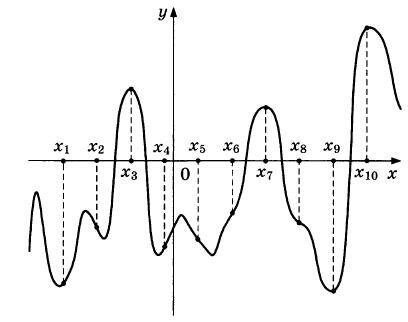 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многогранники. Измерение геометрических величин. |
| Диагональ основания правильной четырехугольной пирамиды в два раза больше высоты боковой грани, проведенной к стороне основания пирамиды. Найдите угол между плоскостями несмежных боковых граней пирамиды. Ответ дайте в градусах. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многогранники. Измерение геометрических величин. |
| Боковое ребро правильной треугольной пирамиды равно 10 и образует с плоскостью основания угол, синус которого равен 0,8. Найдите высоту основания пирамиды. |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
| Расстояние между скрещивающимися ребрами правильной треугольной пирамиды равно 12, а синус угла между боковым ребром и плоскостью основания равен 0,3. Найдите высоту основания пирамиды. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многогранники. Измерение геометрических величин. |
| Тангенс угла между боковым ребром правильной четырехугольной пирамиды и плоскостью ее основания равен ?2 . Найдите тангенс угла между плоскостью боковой грани и плоскостью основания пирамиды. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многогранники. Измерение геометрических величин. |
| Высота основания правильной треугольной пирамиды равна 9, а высота боковой грани пирамиды, проведенная к ребру основания, равна \(\sqrt{73}\) . Найдите боковое ребро пирамиды. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многогранники. Измерение геометрических величин. |
| Сторона основания правильной треугольной пирамиды равна \(10\sqrt{3}\) , а высота пирамиды равна 7. Найдите тангенс угла между боковым ребром и основанием пирамиды. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многогранники. Измерение геометрических величин. |
| Высота PH боковой грани PCD правильной четырехугольной пирамиды PABCD равна \(4\sqrt{3}\) и равна стороне CD основания пирамиды. Найдите расстояние между прямыми АВ и PH. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многогранники. Измерение геометрических величин. |
| Сторона основания правильной четырехугольной пирамиды вдвое больше ее высоты. Найдите угол между плоскостью боковой грани и плоскостью основания пирамиды. Ответ дайте в градусах. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многогранники. Измерение геометрических величин. |
| Тангенс угла между плоскостью боковой грани и плоскостью основания правильной четырехугольной пирамиды равен \(3\sqrt{2}\) . Найдите тангенс угла между боковым ребром и плоскостью основания пирамиды. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многогранники. Измерение геометрических величин. |
| Высота правильной четырехугольной пирамиды равна 12, а сторона основания равна 8. Найдите тангенс угла между плоскостью боковой грани и плоскостью основания пирамиды. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Элементы теории вероятностей. |
| В сборнике билетов по биологии всего 25 билетов, в 12 из них встречается вопрос по круглым червям. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику попадется вопрос по круглым червям. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Элементы теории вероятностей. |
| Конкурс исполнителей проводится в 3 дня. Всего заявлено 80 выступлений — по одному от каждой страны. В первый день запланировано 20 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьевкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса? |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
| На соревнования по метанию диска приехали 6 спортсменов из Швейцарии, 3 из Болгарии и 6 из Австрии. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что третьим будет выступать спортсмен из Болгарии. |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
|
|
| Элементы теории вероятностей. |
| В классе 7 мальчиков и 14 девочек. 1 сентября случайным образом определяют двух дежурных на 2 сентября, которые должны приготовить класс к занятиям. Найдите вероятность того, что будут дежурить два мальчика. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Элементы теории вероятностей. |
| В каждой двадцать пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Коля покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Коля не найдет приз в своей банке. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Элементы теории вероятностей. |
| Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвуют 56 шашистов, среди которых 12 участников из России, в том числе Валерий Стремянкин. Найдите вероятность того, что в первом туре Валерий Стремянкин будет играть с каким-либо шашистом из России. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Элементы теории вероятностей. |
| Перед началом матча по футболу судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Белые» по очереди играет с командами «Красные», «Синие» и «Зеленые». Найдите вероятность того, что ровно в одном матче право первой владеть мячом получит команда «Белые». |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Элементы теории вероятностей. |
| Марина и Дина бросают кубик по одному разу. Выигрывает та девочка, у которой выпадет больше очков. Первой кубик бросила Марина, у нее выпало 3 очка. Найдите вероятность того, что Дина выиграет. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Элементы теории вероятностей. |
| В группе по английскому языку учатся 10 школьников: Антон, Вадик, Галя, Даша, Игорь, Коля, Люда, Митя, Полина, Ярослав. В начале урока учительница произвольным образом выбирает ученика, чтобы он отвечал домашнее задание у доски. Найдите вероятность того, что к доске пойдет мальчик. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Тригонометрические уравнения |
Решите уравнение
\( 3 sin^{2} х + 5 sin x + 2 = 0 \)
и найдите корни, принадлежащие отрезку
\( \left[ \frac{\pi}{2} ; 2\pi \right] \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
|
|
| Тригонометрические уравнения |
Решите уравнение
\( \frac{(tg x + \sqrt{3} ) log_{13} ( 2sin^{2} x)}{log_{31} (\sqrt{2} cos x)} = 0 \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Тригонометрические уравнения |
Решите уравнение
\(6 sin^{2} x - 5 sin x - 4 = 0 \)
и найдите корни, принадлежащие отрезку
\( \left[ - \frac{7\pi}{2} ; - \frac{3\pi}{2} \right] \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Тригонометрические уравнения |
Решите уравнение
\(tg^{2} x + 5 tg x + 6 = 0\)
найдите корни, принадлежащие отрезку
\(\left[ -2\pi ; - \frac{\pi}{2} \right] \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
|
|
| Тригонометрические уравнения |
Решите уравнение
\( 7 sin^{2} x + 8 cos x - 8 = 0\)
и найдите корни, принадлежащие отрезку
\( \left[ - \frac{\pi}{4} ; \frac{\pi}{4} \right] \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
|
|
| Тригонометрические уравнения |
Решите уравнение
\(5 cos^{2} х - 12 cos х + 4 = 0 \)
и найдите корни, принадлежащие отрезку
\( \left[ - \frac{5\pi}{2} ; - \pi \right] \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Тригонометрические уравнения |
Решите уравнение
\(6 sin^{2} x + 7 cos x - 7 = 0 \)
и найдите корни, принадлежащие отрезку
\( \left[ -3\pi ; - \pi \right] \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Углы и расстояния в пространстве |
| Основанием прямой треугольной призмы ABCA1B1C1 является равнобедренный треугольник ABC, в котором АВ = ВС = 20, АС = 32. Боковое ребро призмы равно 24. Точка Р принадлежит ребру BB1 причем ВР : РВ1 = 1:3. Найдите тангенс угла между плоскостями A1B1C1 и АСР. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Углы и расстояния в пространстве |
| Основание прямой четырехугольной призмы A...D1 — прямоугольник ABCD, в котором АВ = 5, AD = ?11. Найдите тангенс угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD перпендикулярно прямой BD1 если расстояние между прямыми АС и B1D1 равно 12. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Углы и расстояния в пространстве |
| В правильной шестиугольной призме A...F1 все ребра которой равны 1, найдите тангенс угла между плоскостями ABC и DB1F1. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Углы и расстояния в пространстве |
| В правильной шестиугольной призме A..F1, все ребра которой равны 1, найдите расстояние от точки А до плоскости DEA1. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Углы и расстояния в пространстве |
| Ребро AD пирамиды DABC перпендикулярно плоскости основания ABC. Найдите расстояние от вершины А до плоскости, проходящей через середины ребер АВ, АС и AD, если AD = \(2\sqrt{5}\) , АВ = АС =10, ВС = \(4\sqrt{5}\). |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Углы и расстояния в пространстве |
| В пирамиде DABC известны длины ребер: АВ = АС = DB = DC = 10, ВС = DA =12. Найдите расстояние между прямыми DA и ВС. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Углы и расстояния в пространстве |
| Основанием прямой треугольной призмы АВСА1В1С1 является равнобедренный треугольник ABC, в котором АВ = ВС = 10, АС = 16. Боковое ребро призмы равно 24. Точка Р — середина ребра ВВ1. Найдите тангенс угла между плоскостями A1B1C1 и АСР. |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
|
|
| Углы и расстояния в пространстве |
| В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины ребер: АА1 = 5, АВ = 12, AD — 8. Найдите тангенс угла между плоскостью ABC и плоскостью, проходящей через точку В перпендикулярно прямой АК, если К — середина ребра C1D1. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Углы и расстояния в пространстве |
| В правильной треугольной призме ABCA1B1C1 ребро основания АВ = \(8\sqrt{3}\) , а боковое ребро АА1 = 7. Найдите тангенс угла между плоскостями BCA1 и BB1C1. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Неравенства, содержащие знак корня или логарифма |
Решите неравенство
\( \frac{3 log_{2} x}{2 + log_{2} x} \leq 2 log_{2} x - 1 \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Неравенства, содержащие знак корня или логарифма |
Решите систему неравенств:
\( \left\{ \begin{eqnarray} 4^{x} - 12 \cdot 2^{x} + 32 \geq 0, \\ \log_{x}(x - 2) \cdot \log_{x}(x+2) \leq 0. \\ \end{eqnarray} \right. \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Неравенства, содержащие знак корня или логарифма |
Решите систему неравенств
\( \left\{ \begin{eqnarray} x^{2} + 6^{x} + 4 \leq 44 \cdot \log_{5} (x+3), \\ 4x + 6^{x} \geq 44 \cdot \log_{5} (x+3). \\ \end{eqnarray} \right. \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Неравенства, содержащие знак корня или логарифма |
Решите неравенство
\(log_{\frac{25-x^{2}}{16}} \frac{24 + 2x - x^{2}}{14} > 1\) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Неравенства, содержащие знак корня или логарифма |
Решите систему неравенств:
\( \left\{ \begin{eqnarray} 4^{x+1} - 17 \cdot 2^{x} + 4 \leq 0, \\ \log^{2}_{|x|}(x^2) + log_{2} (x^2) \leq 8. \\ \end{eqnarray} \right. \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Неравенства, содержащие знак корня или логарифма |
Решите систему неравенств:
\( \left\{ \begin{eqnarray} 4 log_{9} (x + 4,5) - 1 \geq 3^{4x^{2}-9}, \\ 3 - 4 log_{9} (x + 4,5) \geq 3^{9-4x^{2}}. \\ \end{eqnarray} \right. \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Неравенства, содержащие знак корня или логарифма |
Решите неравенство
\( log^{2}_{x+2} (x - 18)^{2} + 32 \leq 16 log_{x+2} (36 + 16x - x^{2}) \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
|
|
|
|
|
|
|
|
| Многоконфигурационная планиметрическая задача |
| Медиана AM и биссектриса CD прямоугольного треугольника ABC (B= 90°) пересекаются в точке О. Найдите площадь треугольника ABC, если СО = 9, OD = 5. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многоконфигурационная планиметрическая задача |
| В равнобедренном треугольнике основание и боковая сторона равны соответственно 5 и 20. Найдите биссектрису угла при основании треугольника. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многоконфигурационная планиметрическая задача |
| На сторонах АВ, ВС и АС треугольника ABC взяты соответственно точки К, L и М, причем АК : КВ = 2:3, BL : LC = 1:2, СМ : МА = 3 : 1. В каком отношении отрезок KL делит отрезок ВМ? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многоконфигурационная планиметрическая задача |
| Окружность, построенная на стороне АС треугольника ABC как на диаметре, проходит через середину стороны ВС и пересекает в точке D продолжение стороны АВ за точку А, причем AD = 2/3 АВ. Найдите площадь треугольника ABC, если АС = 1. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многоконфигурационная планиметрическая задача |
| Окружности радиусов 2 и 4 касаются в точке В. Через точку В проведена прямая, пересекающая второй раз меньшую окружность в точке А, а большую — в точке С. Известно, что АС = 3. Найдите ВС. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многоконфигурационная планиметрическая задача |
| Окружности S1 и S2 радиусов R и r (R > r) соответственно касаются в точке А. Через точку В, лежащую на окружности S1, проведена прямая, касающаяся окружности S2 в точке М. Найдите ВМ, если известно, что АВ = а. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многоконфигурационная планиметрическая задача |
| Точка О — центр окружности радиуса 2. На продолжении радиуса ОМ взята точка А. Через точку А проведена прямая, касающаяся окружности в точке К. Известно, что угол OAK= 60°. Найдите радиус окружности, вписанной в угол ОАК и касающейся данной окружности внешним образом. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многоконфигурационная планиметрическая задача |
| Дана окружность радиуса 2 с центром О. Хорда АВ пересекает радиус ОС в точке D, причем угол CDA= 120°. Найдите радиус окружности, вписанной в угол ADC и касающейся дуги АС, если OD = \(\sqrt{3}\). |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многоконфигурационная планиметрическая задача |
| Окружности с центрами О и B радиуса ОВ пересекаются в точке С. Радиус ОА окружности с центром О перпендикулярен ОВ, причем точки А и С лежат по одну сторону от прямой ОВ. Окружность S1 касается меньших дуг АВ и ОС этих окружностей, а также прямой ОА, а окружность S2 касается окружности с центром В, прямой ОА и окружности S1. Найдите отношение радиуса окружности S1 к радиусу окружности S2. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Многоконфигурационная планиметрическая задача |
| Дан параллелограмм со сторонами 1 и 2 и острым углом 60°. На двух его сторонах как на основаниях построены вне параллелограмма равнобедренные треугольники с углами 120° при вершинах. Найдите расстояние между этими вершинами. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Уравнения, неравенства, системы с параметром |
Найдите значения параметра а, для каждого из которых при любом значении параметра b имеет хотя бы одно решение система уравнений:
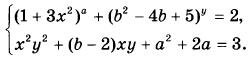 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Уравнения, неравенства, системы с параметром |
Найдите все пары чисел а и b, для каждой из которых имеет не менее пяти решений (х; у) система уравнений
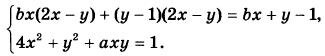 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Уравнения, неравенства, системы с параметром |
Найдите все значения параметра а, при каждом из которых имеет единственное решение (х; у) система уравнений
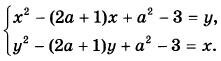 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Уравнения, неравенства, системы с параметром |
Найдите все значения параметра а, при каждом из которых модуль разности корней уравнения
\(х^{2} - 6х + 12 + а^{2} - 4а = 0\)
принимает наибольшее значение. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Уравнения, неравенства, системы с параметром |
Найдите все значения параметра а, при каждом из которых система уравнений
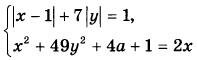
имеет ровно четыре решения. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Уравнения, неравенства, системы с параметром |
Найдите все значения параметра а, при каждом из которых имеет единственное решение система уравнений
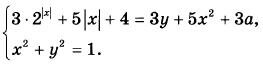 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Уравнения, неравенства, системы с параметром |
Найдите все значения параметра а, при каждом из которых имеет единственное решение система уравнений
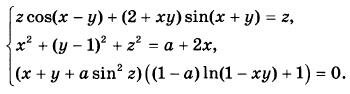 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Уравнения, неравенства, системы с параметром |
Найдите все значения параметра а, при каждом из которых имеет единственное решение система уравнений
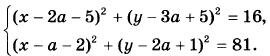 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Уравнения, неравенства, системы с параметром |
Найдите все значения параметра а, при каждом из которых имеет ровно три решения система уравнений
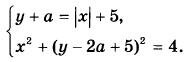 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Уравнения, неравенства, системы с параметром |
Найдите все пары значений параметров а, Ь, при каждой из которых имеет единственное решение система
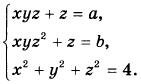 |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа и их свойства |
Найдите все пары натуральных чисел k < n, удовлетворяющие уравнению
\( (\sqrt{n})^{k} = (\sqrt{k})^{n} \) |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа и их свойства |
| Десятичная запись натурального числа п должна состоять из различных (не менее двух) цифр одной четности, а само оно должно быть квадратом целого числа. Найдите все такие n. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа и их свойства |
Найдите наименьшее и наибольшее натуральные значения n, при которых уравнение
\((х^{2} + у^{2})^{2010} = х^{n} • у^{n} \)
имеет натуральные решения. |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
|
|
| Числа и их свойства |
| Квадратный трехчлен f(x) = х2 + рх + q имеет два различных целых корня. Один из корней трехчлена и его значение в точке х = 11 являются простыми числами. Найдите корни трехчлена. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа и их свойства |
| Найдите все такие натуральные n, что при вычеркивании первой цифры у числа \(4^{n}\) снова получается число, являющееся натуральной степенью числа 4. |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа и их свойства |
| Какое наибольшее количество чисел можно выбрать из отрезка натурального ряда от 1 до 2009, так чтобы разность любых двух из них не была простой? |
| Подробнее | Комментировать | Сохранить |
|
|
|
| Числа и их свойства |
Найдите все такие целые а и b, что корни уравнения
\( x^2 + (2a+9) x + 3b + 5 = 0 \)
являются различными целыми числами, а коэффициенты 2а + 9 и Зb + 5 — простыми числами. |
| Подробнее | Комментировать | Сохранить |
|
|
|
|
|
|
| Числа и их свойства |
| Друг за другом подряд выписали десятичную запись чисел \(2^{50}\) и \(5^{50}\). Сколько всего цифр выписали? |
| Подробнее | Комментировать | Сохранить |
|