Тип
|
Задание
|
B1
|
| Школа закупает книги по цене 50 рублей за штуку. При покупке больше 10 штук магазин дает скидку 10%. Сколько книг можно купить на 1000 рублей? |
|
B2
|
На диаграмме показана среднемесячная температура воздуха в Париже за каждый месяц 2009 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев в 2009 году, когда среднемесячная температура была равна 10 градусам Цельсия.
 |
|
B3
|
Найдите площадь параллелограмма ABCD.
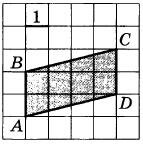 |
|
B4
|
Строительная фирма собирается приобрести 85 кубометров пеноб-локов у одного из трех поставщиков. Цены на пеноблоки и условия доставки приведены в таблице. Какова наименьшая стоимость такой покупки с доставкой (в рублях)?
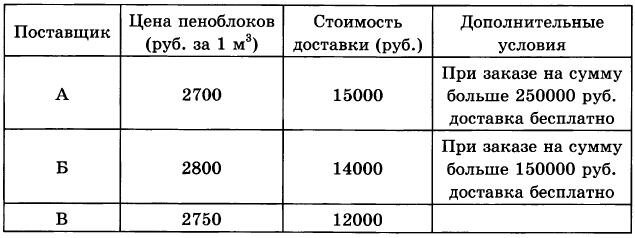 |
|
B5
|
Решите уравнение
\(\sqrt{7-x} = 4 \) |
|
B6
|
| Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК = 7, СК = 8. |
|
B7
|
Вычислите
\(log_{5} 135 - log_{5} 5,4\) |
|
B8
|
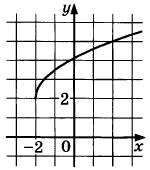
На рисунке изображен график функции у = f(x). Прямая, проходящая через точку (-2; 4), касается этого графика в точке с абсциссой 2. Найдите f'(2).
 |
|
B9
|
| Диагональ основания правильной четырехугольной пирамиды в два раза больше высоты боковой грани, проведенной к стороне основания пирамиды. Найдите угол между плоскостями несмежных боковых граней пирамиды. Ответ дайте в градусах. |
|
B10
|
| В сборнике билетов по биологии всего 25 билетов, в 12 из них встречается вопрос по круглым червям. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику попадется вопрос по круглым червям. |
|
B11
|
| Площадь полной поверхности данного правильного тетраэдра равна 80 см2. Найдите площадь полной поверхности правильного тетраэдра, ребро которого в 4 раза меньше ребра данного тетраэдра. Ответ дайте в см2. |
|
B12
|
| Высоту над землей подброшенного вверх камня можно вычислять по формуле h(t) = 1,6 + 13t - 5t2, где t — время с момента броска в секундах, h — высота в метрах. Сколько секунд камень будет находиться на высоте более 6 метров? |
|
B13
|
| Товарный поезд, идущий со скоростью 30 км/ч, проезжает мимо придорожного столба за 36 секунд. Определите длину поезда (в метрах). |
|
B14
|
Найдите наибольшее значение функции у = 11x + cos х + 10 на отрезке
\(\left[- \frac{\pi}{2} ; 0 \right]\) |
|
C1
|
Решите уравнение
\( 3 sin^{2} х + 5 sin x + 2 = 0 \)
и найдите корни, принадлежащие отрезку
\( \left[ \frac{\pi}{2} ; 2\pi \right] \) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C2
|
| Основанием прямой треугольной призмы ABCA1B1C1 является равнобедренный треугольник ABC, в котором АВ = ВС = 20, АС = 32. Боковое ребро призмы равно 24. Точка Р принадлежит ребру BB1 причем ВР : РВ1 = 1:3. Найдите тангенс угла между плоскостями A1B1C1 и АСР. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C3
|
Решите неравенство
\( \frac{3 log_{2} x}{2 + log_{2} x} \leq 2 log_{2} x - 1 \) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C4
|
| Медиана AM и биссектриса CD прямоугольного треугольника ABC (B= 90°) пересекаются в точке О. Найдите площадь треугольника ABC, если СО = 9, OD = 5. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C5
|
Найдите значения параметра а, для каждого из которых при любом значении параметра b имеет хотя бы одно решение система уравнений:
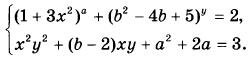 |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C6
|
Найдите все пары натуральных чисел k < n, удовлетворяющие уравнению
\( (\sqrt{n})^{k} = (\sqrt{k})^{n} \) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|