Тип
|
Задание
|
B1
|
| Больному прописан курс лекарства, которое нужно принимать по 250 мг два раза в день в течение 7 дней. В одной упаковке лекарства содержится 10 таблеток по 125 мг. Какое наименьшее количество упаковок понадобится на весь курс лечения? |
|
B2
|
На диаграмме показано число запросов со словом ЕГЭ, сделанных на некотором поисковом сайте во все месяцы с января по декабрь 2009 года. По горизонтали указываются месяцы, по вертикали — число запросов за данный месяц. Определите по диаграмме, во сколько раз максимальное месячное число запросов превышало минимальное месячное число запросов со словом ЕГЭ в 2009 году.
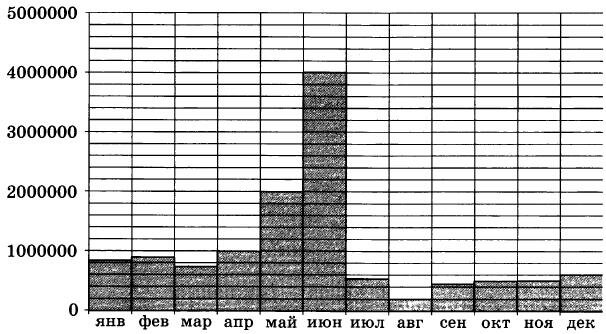 |
|
B3
|
Найдите площадь трапеции ABCD.
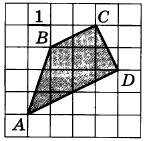 |
|
B4
|
На рисунке показаны схема дорог и расстояние в километрах между населенными пунктами А, В, С, D и Е вдоль этих дорог. Мопед, грузовик и автобус одновременно выезжают из города А и добираются в город Е разными путями. Мопед едет через поселки С и В, грузовик — только через В, а автобус едет через город D. Мопед был в пути 1 час 20 минут, грузовик — 1 час, а автобус — 1 час 40 минут. Найдите среднюю скорость того транспортного средства, у которого эта скорость наибольшая. Ответ дайте в км/ч.
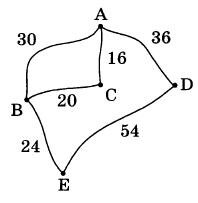 |
|
B5
|
Решите уравнение
\(5^{Х+5} = 0,04\) |
|
B6
|
| Хорды АВ и CD окружности пересекаются в точке М. Найдите МА, если MB = 12, МС = 16, MD = 6. |
|
B7
|
Найдите значение выражения
\(\frac{28}{2^{log_{2} 7}}\) |
|
B8
|
На рисунке изображены график функции у = f(x) и касательная к нему в точке с абсциссой f'(x) Найдите значение производной f(x) в точке x0.
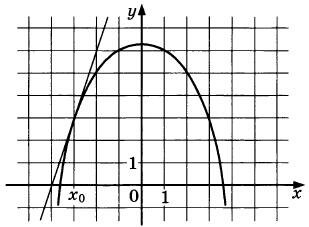 |
|
B9
|
| Тангенс угла между боковым ребром правильной четырехугольной пирамиды и плоскостью ее основания равен ?2 . Найдите тангенс угла между плоскостью боковой грани и плоскостью основания пирамиды. |
|
B10
|
| Найдите вероятность того, что при бросании двух кубиков на каждом выпадет менее 4 очков. |
|
B11
|
| Объем цилиндра равен 20 см3. Радиус основания цилиндра увеличили в 3 раза, а образующую уменьшили в 4 раза. Найдите объем получившегося цилиндра. Ответ дайте в см3. |
|
B12
|
Время полета мяча, брошенного под углом а к плоской горизонтальной поверхности земли, можно посчитать по формуле
\(t = \frac{2V_{0} sin ?}{g}(c)\)
При каком наименьшем значении угла (в градусах) время в полете будет не меньше 2,5 секунды, если мяч бросают с начальной скоростью v0 = 25 м/с? Ускорение свободного падения g считать равным 10 м/с2. |
|
B13
|
| Первую половину трассы автомобиль проехал со скоростью 90 км/ч, а вторую — со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. |
|
B14
|
Найдите наибольшее значение функции
\(у = \frac{54}{\pi} x + 6 sin x + 13 \)
на отрезке
\( \left[ - \frac{5\pi}{6} ; 0 \right] \) |
|
C1
|
Решите уравнение
\(6 sin^{2} x - 5 sin x - 4 = 0 \)
и найдите корни, принадлежащие отрезку
\( \left[ - \frac{7\pi}{2} ; - \frac{3\pi}{2} \right] \) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C2
|
| В правильной шестиугольной призме A..F1, все ребра которой равны 1, найдите расстояние от точки А до плоскости DEA1. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C3
|
Решите неравенство
\(log_{\frac{25-x^{2}}{16}} \frac{24 + 2x - x^{2}}{14} > 1\) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C4
|
| Окружность, построенная на стороне АС треугольника ABC как на диаметре, проходит через середину стороны ВС и пересекает в точке D продолжение стороны АВ за точку А, причем AD = 2/3 АВ. Найдите площадь треугольника ABC, если АС = 1. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C5
|
Найдите все значения параметра а, при каждом из которых модуль разности корней уравнения
\(х^{2} - 6х + 12 + а^{2} - 4а = 0\)
принимает наибольшее значение. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C6
|
| Известно, что при любом целом К ? 27 число а - К3 делится без остатка на 27 - К. Найдите а. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|