Тип
|
Задание
|
B1
|
| Школа закупает книги по цене 70 рублей за штуку. При покупке на сумму больше 500 рублей магазин дает скидку 10%. Сколько рублей будет стоить покупка 23 книг? |
|
B2
|
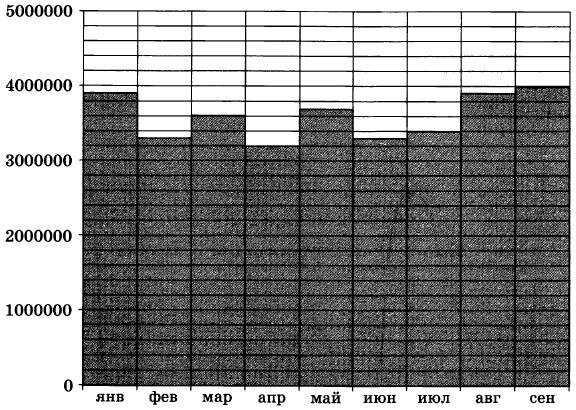
На диаграмме показано число запросов со словом КИНО, сделанных на некотором поисковом сайте во все месяцы с января по сентябрь 2010 года. По горизонтали указываются месяцы, по вертикали — число запросов за данный месяц. Определите по диаграмме наибольшее месячное число запросов со словом КИНО в указанный период.
 |
|
B3
|
Найдите площадь S круга. В ответе укажите \(\frac{S}{\pi}\)
 |
|
B4
|
При заказе дисков в некотором шведском музыкальном магазине цена одного диска не зависит от количества дисков в заказе, а доставка заказа в другие страны осуществляется на таких условиях:
доставка заказа не более чем из трех дисков — 6 $;
доставка заказа от 4 до 8 дисков — 17,5 $;
доставка заказа из 9 и более дисков — 28 $.
Сколько долларов придется заплатить за доставку самым дешевым способом (можно в несколько заказов) при приобретении ровно 9 дисков? |
|
B5
|
Решите уравнение
\(\sqrt{x+4} = 7\) |
|
B6
|
| В прямоугольном треугольнике высота, проведенная к гипотенузе, делит прямой угол на два угла, один из которых равен 56°. Найдите меньший угол данного треугольника. Ответ дайте в градусах. |
|
B7
|
Найдите значение выражения
\(log_{6} 126 - log_{6} 3,5 \) |
|
B8
|
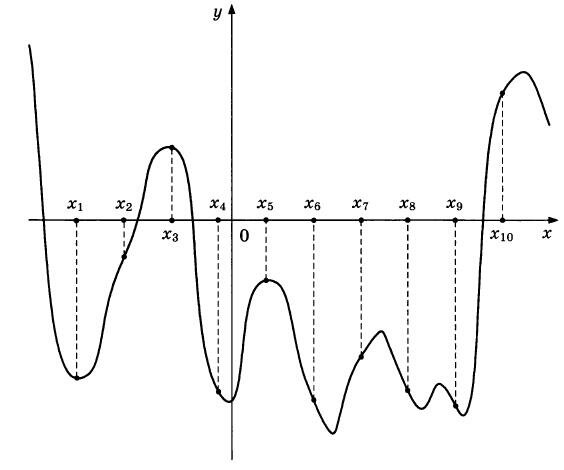
На рисунке изображены график функции у = f(x) и десять точек на оси абсцисс: х1, х2, x3..,x10 В скольких из этих точек производная функции f(x) отрицательна?
 |
|
B9
|
| Высота основания правильной треугольной пирамиды равна 9, а высота боковой грани пирамиды, проведенная к ребру основания, равна \(\sqrt{73}\) . Найдите боковое ребро пирамиды. |
|
B10
|
| В классе 7 мальчиков и 14 девочек. 1 сентября случайным образом определяют двух дежурных на 2 сентября, которые должны приготовить класс к занятиям. Найдите вероятность того, что будут дежурить два мальчика. |
|
B11
|
| Объем цилиндра равен 24 см3. Радиус основания цилиндра уменьшили в 2 раза, а образующую увеличили в 5 раз. Найдите объем получившегося цилиндра. Ответ дайте в см3. |
|
B12
|
| Для одного из предприятий-монополистов зависимость объема спроса на продукцию q (единиц в месяц) от ее цены р (тыс. руб.) задается формулой: q = 100 - 10р. Определите максимальный уровень цены р (в тыс. руб.), при котором значение выручки предприятия за месяц г = q • р составит не менее 210 тыс. руб. |
|
B13
|
| Первая труба наполняет бак объемом 600 литров, а вторая труба — бак объемом 900 литров. Известно, что одна из труб пропускает в минуту на 3 л воды больше, чем другая. Сколько литров воды в минуту пропускает вторая труба, если баки были наполнены за одно и то же время? |
|
B14
|
Найдите наименьшее значение функции у = 11 tg х - 11x + 16 на отрезке
\(\left[ 0 ; \frac{\pi}{4} \right] \) |
|
C1
|
Решите уравнение
\(tg^{2} x + 5 tg x + 6 = 0\)
найдите корни, принадлежащие отрезку
\(\left[ -2\pi ; - \frac{\pi}{2} \right] \) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C2
|
| Ребро AD пирамиды DABC перпендикулярно плоскости основания ABC. Найдите расстояние от вершины А до плоскости, проходящей через середины ребер АВ, АС и AD, если AD = \(2\sqrt{5}\) , АВ = АС =10, ВС = \(4\sqrt{5}\). |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C3
|
Решите систему неравенств:
\( \left\{ \begin{eqnarray} 4^{x+1} - 17 \cdot 2^{x} + 4 \leq 0, \\ \log^{2}_{|x|}(x^2) + log_{2} (x^2) \leq 8. \\ \end{eqnarray} \right. \) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C4
|
| Окружности радиусов 2 и 4 касаются в точке В. Через точку В проведена прямая, пересекающая второй раз меньшую окружность в точке А, а большую — в точке С. Известно, что АС = 3. Найдите ВС. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C5
|
Найдите все значения параметра а, при каждом из которых система уравнений
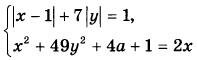
имеет ровно четыре решения. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C6
|
| Квадратный трехчлен f(x) = х2 + рх + q имеет два различных целых корня. Один из корней трехчлена и его значение в точке х = 11 являются простыми числами. Найдите корни трехчлена. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|