Тип
|
Задание
|
B1
|
| В туристический поход на 7 дней отправляется группа из 8 человек. В походе на одного человека приходится 90 грамм сахара в день. Сколько трехкилограммовых мешков сахара нужно купить, чтобы сахара хватило на весь поход? |
|
B2
|
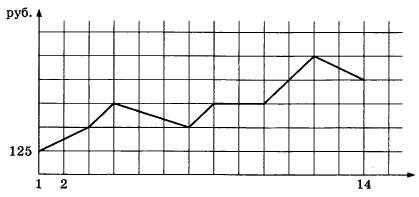
На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций газодобывающей компании в первые две недели апреля. В первую неделю апреля бизнесмен купил 14 акций, а потом продал их на второй неделе. Какую наибольшую прибыль он мог получить? Ответ дайте в рублях.
 |
|
B3
|
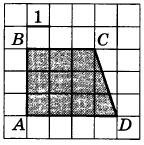
Найдите площадь трапеции ABCD.
 |
|
B4
|
Строительной фирме нужно приобрести 60 кубометров пеноблоков у одного из трех поставщиков. Какова наименьшая стоимость (в рублях) покупки с доставкой, если цены на пеноблоки и условия доставки приведены в таблице?
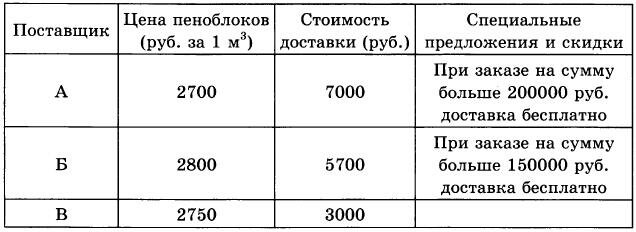 |
|
B5
|
Решите уравнение
\(log_{25} (2-3x) = 0,5 \) |
|
B6
|
| Концы отрезка АВ лежат по разные стороны от прямой l. Расстояние от точки А до прямой l равно 7, а расстояние от точки В до прямой l равно 13. Найдите расстояние от середины отрезка АВ до прямой l. |
|
B7
|
| Найдите значение выражения \(\frac{60}{6^{log_{6} 5}}\) |
|
B8
|
На рисунке изображен график функции у = f(x) и отмечены точки -5, -3, 3, 7. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
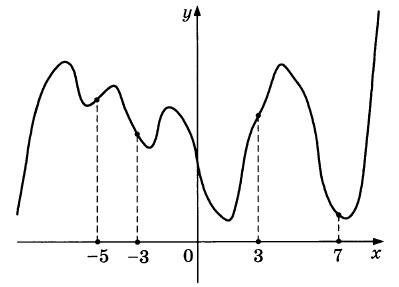 |
|
B9
|
| Сторона основания правильной треугольной пирамиды равна \(10\sqrt{3}\) , а высота пирамиды равна 7. Найдите тангенс угла между боковым ребром и основанием пирамиды. |
|
B10
|
| В каждой двадцать пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Коля покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Коля не найдет приз в своей банке. |
|
B11
|
| Объем данной правильной треугольной призмы равен 80 см. Найдите объем правильной треугольной призмы, ребро основания которой в 4 раза меньше ребра основания данной призмы, а высота в 4 раза больше высоты данной призмы. Ответ дайте в см3. |
|
B12
|
Для поддержания навеса планируется использовать цилиндрическую колонну. Давление (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле
\(Р = \frac{4mg}{\pi D^{2}} \)
где m = 2700 кг - их общая масса, D (в метрах) — диаметр колонны. Считая ускорение свободного падения g равным 10 м/с2, а ? равным 3, определите наименьший возможный диаметр колонны (в метрах), если давление, оказываемое на опору, не должно быть больше 400000 Па. |
|
B13
|
| Три килограмма черешни стоят столько же, сколько пять килограммов вишни, а три килограмма вишни — столько же, сколько два килограмма клубники. На сколько процентов килограмм клубники дешевле килограмма черешни? |
|
B14
|
Найдите наибольшее значение функции
\( y = 12 tg x - 12 x + 3\pi - 13 \)
на отрезке
\( \left[ - \frac{\pi}{4} ; \frac{\pi}{4} \right] \) |
|
C1
|
Решите уравнение
\( \frac{3 ctg^{2} x + 4 ctg x}{5 cos^{2} x - 4 cos x} = 0 \) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C2
|
| В пирамиде DABC известны длины ребер: АВ = АС = DB = DC = 10, ВС = DA =12. Найдите расстояние между прямыми DA и ВС. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C3
|
Решите систему неравенств:
\( \left\{ \begin{eqnarray} 4 log_{9} (x + 4,5) - 1 \geq 3^{4x^{2}-9}, \\ 3 - 4 log_{9} (x + 4,5) \geq 3^{9-4x^{2}}. \\ \end{eqnarray} \right. \) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C4
|
| Окружности S1 и S2 радиусов R и r (R > r) соответственно касаются в точке А. Через точку В, лежащую на окружности S1, проведена прямая, касающаяся окружности S2 в точке М. Найдите ВМ, если известно, что АВ = а. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C5
|
Найдите все значения параметра а, при каждом из которых имеет единственное решение система уравнений
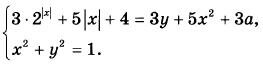 |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C6
|
| Найдите все такие натуральные n, что при вычеркивании первой цифры у числа \(4^{n}\) снова получается число, являющееся натуральной степенью числа 4. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|