Тип
|
Задание
|
B1
|
| В двух автомобилях перевозилось одинаковое количество помидоров. При этом в первом автомобиле при транспортировке испортилось 20% перевозимых помидоров, что составило 96 штук. Во втором автомобиле испортилось 15% помидоров. Сколько помидоров испортилось во втором автомобиле? |
|
B2
|
На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций газодобывающей компании в первые две недели ноября. 2 ноября бизнесмен приобрел 10 акций этой компании. Шесть из них он продал 6 ноября, а 13 ноября — остальные 4. Сколько рублей потерял бизнесмен в результате этих операций?
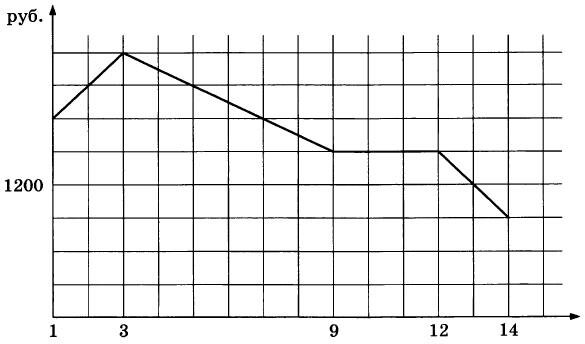 |
|
B3
|
Найдите площадь прямоугольника ABCD.
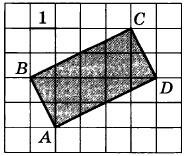 |
|
B4
|
При заказе дисков в некотором шведском музыкальном магазине цена одного диска не зависит от количества дисков в заказе, а доставка заказа в другие страны осуществляется на таких условиях:
доставка заказа не более чем из трех дисков — 6 $;
доставка заказа от 4 до 8 дисков — 17,5 $;
доставка заказа из 9 и более дисков — 28 $.
Сколько долларов придется заплатить за доставку самым дешевым способом (можно в несколько заказов) при приобретении ровно 11 дисков? |
|
B5
|
Решите уравнение
\(\sqrt{x+9} = 5 \) |
|
B6
|
| Диагонали трапеции AJBCD с основаниями АВ и CD пересекаются в точке М. Найдите МС, если АВ = 11, DC = 33, АС = 28. |
|
B7
|
Найдите значение выражения
\(log_{6} 144 - log_{6} 4 \) |
|
B8
|
На рисунке изображен график функции у = f(x). Прямая, проходящая через точку (-6; -1), касается этого графика в точке с абсциссой 6. Найдите f(6).
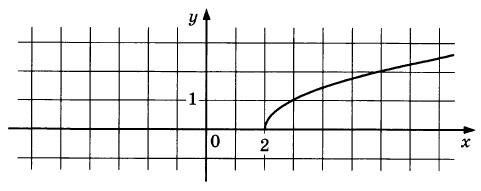 |
|
B9
|
| Сторона основания правильной четырехугольной пирамиды вдвое больше ее высоты. Найдите угол между плоскостью боковой грани и плоскостью основания пирамиды. Ответ дайте в градусах. |
|
B10
|
| Перед началом матча по футболу судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Белые» по очереди играет с командами «Красные», «Синие» и «Зеленые». Найдите вероятность того, что ровно в одном матче право первой владеть мячом получит команда «Белые». |
|
B11
|
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания цилиндра равен 2. Объем параллелепипеда равен 80. Найдите высоту цилиндра.
 |
|
B12
|
Масса радиоактивного вещества уменьшается по закону
\(m(t) = m_{0} \cdot 2^{-\frac{t}{T}} \)
В лаборатории получили вещество, содержащее в начальный момент времени m0 = 280 мкг изотопа железа-59, период полураспада которого Т =45 суток. В течение скольких суток содержание изотопа железа-59 в веществе будет превосходить 17,5 мкг? |
|
B13
|
| Имеются два сосуда, содержащие 42 кг и 6 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 40% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 50% кислоты. Сколько килограммов кислоты содержится в первом растворе? |
|
B14
|
Найдите наибольшее значение функции
\( у = (21 - x) е^{20-x} \)
на отрезке [19; 21]. |
|
C1
|
Решите уравнение
\(\frac{log_{5} (-2 cos x)}{\sqrt{5 tg x}} = 0 \) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C2
|
| Дан куб ABCDA1B1C1D1. Найдите угол между плоскостями АВ1С1 и А1B1С. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C3
|
Решите неравенство
\( log_{2-x} (x+2) \cdot log_{x+3} (3-x) \leq 0 \) |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C4
|
| Дана окружность радиуса 2 с центром О. Хорда АВ пересекает радиус ОС в точке D, причем угол CDA= 120°. Найдите радиус окружности, вписанной в угол ADC и касающейся дуги АС, если OD = \(\sqrt{3}\). |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C5
|
Найдите все значения параметра а, при каждом из которых имеет единственное решение система уравнений
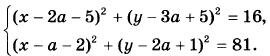 |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|
C6
|
Найдите все такие целые а и b, что корни уравнения
\( x^2 + (2a+9) x + 3b + 5 = 0 \)
являются различными целыми числами, а коэффициенты 2а + 9 и Зb + 5 — простыми числами. |
| Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям |
|