Правильный ответ:
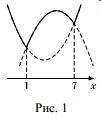
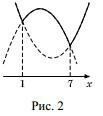
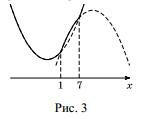
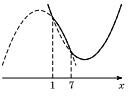
1. Функция \(f\) имеет вид:
а) при \(x^2 - 8x + 7 \geq 0\):
\(f(x) = x^2 +2(a-4)x + 7\),
а её график есть две части параболы с ветвями, направленными вверх, и осью симметрии \(x=4-a\);
б) при \(x^2 - 8x + 7 < 0 \):
\(f(x) = -x^2 + (2a+8)x - 7\),
а её график есть часть параболы с ветвями, направленными вниз.
Все возможные виды графика функции \(f(x)\) показаны на рисунках:

2. Наименьшее значение функция \(f(x)\) может принять только в точках \(x=1\) или \(x=7\), если \(4 - a \notin [1; 7]\) - то в точке \(x = 4 - a\).
3. Наименьшее значение функции \(f\) больше 1 тогда и только тогда, когда:
\(\left\{ \begin{eqnarray} f(1)>1, \\ f(7) > 1, \\ f(4-a) > 1 \\ \end{eqnarray} \right. \Leftrightarrow \left\{ \begin{eqnarray} 2a > 1, \\ 14a > 1, \\ 2a(4-a) + |a^2-9| > 1 \\ \end{eqnarray} \right. \Leftrightarrow\)
\(\Leftrightarrow \left\{ \begin{eqnarray} a > \frac{1}{2} \\ a > \frac{1}{14} \\ 2a^2 -8a + 1 - |a^2 - 9| < 0 \\ \end{eqnarray} \right. \Leftrightarrow \left[ \begin{eqnarray} \left\{ \begin{eqnarray} a \geq 3, \\ a^2 - 8a + 10 < 0 \\ \end{eqnarray} \right. \\ \left\{ \begin{eqnarray} \frac{1}{2} < a < 3, \\ 3a^2 - 8a - 8 < 0 \\ \end{eqnarray} \right. \\ \end{eqnarray} \right. \Leftrightarrow \)
\(\Leftrightarrow \left[ \begin{eqnarray} \left\{ \begin{eqnarray} a \geq 3, \\ 4 - \sqrt{6} < a < 4 + \sqrt{6} \\ \end{eqnarray} \right. \\ \left\{ \begin{eqnarray} \frac{1}{2} < a < 3, \\ \frac{4-\sqrt{40}}{3} < a < \frac{4+\sqrt{40}}{3} \\ \end{eqnarray} \right. \\ \end{eqnarray} \right. \Leftrightarrow \left[ \begin{eqnarray} 3 \leq a < 4 + \sqrt{6} \\ \frac{1}{2} < a < 3 \\ \end{eqnarray} \right. \Leftrightarrow\)
\(\Leftrightarrow \frac{1}{2} < a < 4 + \sqrt{6}\)
Ответ: \(\left( \frac{1}{2}; 4 + \sqrt{6} \right)\).