Введение

Во-первых, нужно понимать, что вся информация представляется в памяти компьютера в виде нулей и единичек - в двоичной системе счисления. Мы привыкли считать в десятичной системе счисления - где присутствуют цифры с 0 до 9 (всего 10 цифр - отсюда "десятичная"). По аналогии - в двочиной системе счисления есть только 2 цифры - это 0 и 1. Так же, например, в восьмеричной системе счисления есть цифры с 0 до 7 (всего 8 цифр).

В основном встречаются двоичная, троичная, четверичная, пятиричная, шестиричная, семиричная, восьмеричная, девятиричная, десятичная и шестнадцатеричная системы счисления. Для шестнадцатеричной системы счисления после цифр (0..9) идут первые буквы английского алфавита (A,B,C,D,E,F).

Основные правила

Существуют 2 основных правила для работы с числами в разных системах счисления:

1.     Правило перевода из любой системы в десятичную,

2.     Правило перевода из десятичной в любую.

Эти правила мы сейчас разберем эти правило и вам их необходимо будет выучить, так как на ЕГЭ они очень часто встречаются. Позже мы разберем ещё пару трюков для частых переводов из одной в другую систем счислений.

Правило перевода из любой системы счисления в десятичную

Для перевода числа в десятичную систему счисления из системы счисления с другим основанием каждый коэффициент переводимого числа умножается на основание системы в степени соответствующей этому коэффициенту и полученные результаты складываются.

С первого раза довольно трудно усвоить, поэтому разберем примеры:

Перевести число 1001011011₂  в десятичную систему счисления.

Цифра 2 в нижнем регистре указывает на систему счисления. В данном случае - двоичная. Другими словами, необходимо перевести двоичное число в десятичную систему счисления. 

1001011011₂ = 1*2⁹+0*2⁸+0*2⁷+1*2⁶+0*2⁵+1*2⁴+1*2³+0*2²+1*2¹+1*2⁰ = 512 + 64 + 16 + 8 + 2 = 746₁₀ - ответ: 746.

Перевести число 347₈ в десятичную систему счисления.

347₈ = 3*8³ + 4*8² + 7*8¹ + 7*8⁰ = 1536 + 256 + 56 + 7 = 1855₁₀ - ответ: 1855.

 

Правило перевода из десятичной системы счисления в любую

Для перевода числа в десятичную систему счисления из системы счисления с другим основанием каждый коэффициент переводимого числа умножается на основание системы в степени соответствующей этому коэффициенту и полученные результаты складываются.

И снова примеры:

Перевести число 145₁₀ в систему счисления с основанием 5.

Отсюда ответ: 145₁₀ = 1040₅.

Перевести число 181₁₀ в восьмеричную систему счисления.

Отсюда ответ: 181₁₀ = 265₈.

Перевести число 622₁₀ в шестнадцатеричную систему счисления.

Т.к. цифры с номером 14 не существует, она заменяется буквой согласно таблице 1:

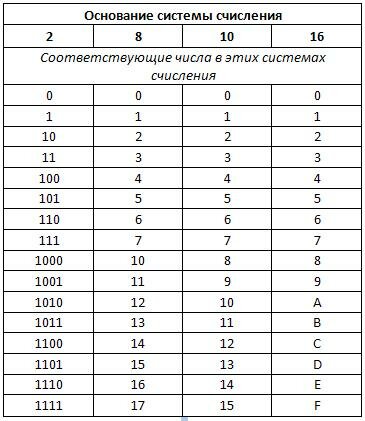
Поэтому ответ будет следующим: 622₁₀ = 26E₁₆.

Правила перевода для частных случаев

Для систем счисления с основаниями 2, 8 и 16 существуют специальные правила, ускоряющие перевод из одной системы счисления в другую.

Правило перевода из шестнадцатеричной системы счисления в двоичную и обратно

Для совершения таких переводов вводится понятие тетрад – это группа из четырех цифр, на которое разбивается двоичное число, которое нужно перевести. Например, если число 1100100110101011₂ перевести в двоичную систему счисления, то получится 4 тетрады: 1100, 1001, 1010, 1011. В таблице 1 (см. выше) смотрим соответствие этих тетрад:

И записываем ответ таким образом:

Примечание: Разбивание на тетрады происходит слева направо и если количество цифр в двоичном числе не кратно четырем, то слева дописываются нули. Пример: число 110010110 записывается как 000110010110 и разбивается на три тетрады: 0001, 1001 и 0110.

Верно и обратный алгоритм. Т.е. если мы хотим перевести шестнадцатеричное число в двоичное, то необходимо каждую цифру/букву преобразовать в соответствующую тетраду. Пример: AC2D₁₆ = 1010110000101101₂.

Правило перевода из восьмеричной системы счисления в двоичную и обратно

Аналогично тетрадам, для быстрых переводов из восьмеричной системы счисления в двоичную и обратно вводится понятие триад – это группа из трех цифр. И правило здесь полностью аналогично предыдущему. К примеру, переведем то же самое число 1100100110101011₂ в восьмеричную систему счисления:

1.     Разобьем на триады: 001, 100, 100, 110, 101, 011.

2.     Найдем соответствие каждой триаде в таблице: 001 – 1, 100 – 4, 110 – 6, 101 – 5, 011 – 3.

3.     Запишем ответ: 1100100110101011₂ = 14653₈.

Также верен и обратный алгоритм.

Полезные советы

Считаю ознакомление с позиционными системами счисления и правилами перевода на этом оконченным. В основном, конечно, в ЕГЭ встречаются системы счисления с основанием 2, 8 и 16. Поэтому приведенную таблицу рекомендуется выучить, но если вы будете много решать примеры, то, 100%, что она у вас и так отложиться в памяти.

Если вы хотите узнать по этой теме больше информации, то можете прочитать следующие статьи по ссылкам:

·         Википедия: Системы счисления.

·         Викиучебник: Системы счисления.

Кроме основных правил существуют ещё небольшие уловки, которые помогают решать специфические задачи. О них я напишу скоро в другой статье под названием «Системы счисления: Продвинутый уровень».

 

Надеюсь, что тебе, читателю эта статья помогла, и ты узнал что-либо новое.

Если тебе ещё предстоит сдать ЕГЭ, то желаю тебе получить МАКСИМУМ баллов,

,

aka Hack.Nick.